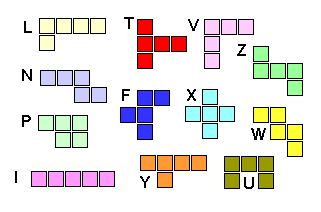Historique▲
- mai-juillet 2007 : création du document
- 10 juillet 2007 : prise en compte de remarques de rédacteurs de Developpez.com ; ajout du perfectionnement concernant les dimensions du plateau
- 09 août 2007 : passage au gabarit du site Developpez.com ; lien vers la liste d'anti-patrons de tests unitaires
I. Introduction▲
Ce tutoriel propose la mise en oeuvre d'un développement dirigé par les tests (Test Driven Development - TDD) sur un cas concret selon les principes exposés par Kent Beck dans son livre Test-Driven Development: By Example.
L'exemple donné par Kent Beck (un calculateur multi-monnaies) est trompeusement simple, si bien que des lecteurs sous-estiment parfois l'intérêt du TDD. Aussi ce tutoriel s'appuie sur un sujet qui paraîtra plus difficile, afin de mieux montrer l'apport du TDD.
- https://smeric.developpez.com/java/astuces/tests/
- https://jab.developpez.com/tutoriels/dotnet/nunit/
nous allons essayer de montrer la mise en pratique de cette démarche de A à Z, afin de bien insister sur la discipline particulière que propose Kent Beck.
Le sujet que nous allons traiter est le calcul de toutes les solutions possibles du jeu des pentaminos (voir wikipedia).
L'objectif est de placer ces douze pentaminos sur un rectangle de 6 par 10 cases, sans aucun trou ni chevauchement. Grâce à wikipedia, nous savons d'avance qu'il y a 2339 solutions uniques (4 fois plus en comptant les solutions symétriques), et dans ce tutoriel nous souhaitons pouvoir les afficher toutes.
Réaliser un tel programme paraît souvent difficile, notamment en raison du caractère "géométrique" du problème, et c'est à ce titre qu'il nous intéresse comme support d'introduction du TDD. De plus ce problème n'est pas uniquement ludique, c'est un cas particulier d'un problème de satisfaction de contraintes qu'un développeur peut être amené à rencontrer ; il est donc intéressant d'en connaître les principes de résolution.
Le projet sera réalisé en Visual C# 2005 Express Edition, téléchargeable gratuitement sur le site de Microsoft (http://www.microsoft.com/france/msdn/vstudio/express/vcsharp/telechargez.mspx) et avec l'aide de l'outil de tests unitaires Nunit, également téléchargeable gratuitement (http://www.Nunit.org/ - prendre la version win .net 2.0).
II. Principes du TDD▲
L'objectif du TDD est de produire du "code propre qui fonctionne". Pour cela, deux principes sont mis en oeuvre :
- un développeur écrit du code nouveau seulement lorsqu'un test automatisé a échoué
- toute duplication de code (ou plus généralement d'information, ou de connaissances) doit être éliminée. L'acronyme anglais DRY (Do not Repeat Yourself) peut être utilisé comme moyen mnémotechnique pour cette phase très importante.
Ces deux principes doivent être strictement respectés, même s'ils paraissent difficiles ou bizarres dans un premier temps. Bien comprendre le TDD suppose en effet de respecter strictement la discipline imposée par le cycle décrit ci-dessous.
- nous allons concevoir notre code de manière incrémentale, en ayant toujours du code en état de marche, de telle sorte que ce code nous fournisse de l'information pour prendre de nombreuses petites décisions au cours de notre développement.
- nous devons écrire nos propres tests, parce que nous ne pouvons pas attendre de nombreuses fois par jour qu'une autre personne le fasse
- notre environnement de développement doit fournir une réponse ultra rapide en cas de petits changements
- notre code doit être composé d'éléments très cohérents et très peu couplés, afin de rendre le test facile.
Le travail se fait en trois phases. Les deux premières sont nommées d'après la couleur de la barre de progrès dans les outils comme Nunit :
- ROUGE: écrire un petit test qui échoue, voire même ne compile pas dans un 1er temps
- VERT : faire passer ce test le plus rapidement possible, en s'autorisant si besoin les "pires" solutions : S'il existe une solution propre, simple et immédiate, réalisez-laSi une telle solution prend plus d'une minute, notez la et revenez au problème principal : avoir une barre de progrès verte en quelques secondes
- REMANIEMENT (refactoring en anglais) : éliminer absolument toute duplication apparue durant les étapes 1 et 2.
- Simulation : retourner une constante, puis remplacer progressivement ces constantes avec des variables afin d'obtenir le code réel
- Implémentation évidente : taper directement la bonne solution
- Triangulation : avoir deux exemples du résultat recherché, et généraliser.
- ajouter rapidement un nouveau test
- Exécuter tous les tests, et constater l'échec du nouveau : ROUGE
- Faire un petit changement
- Exécuter tous les tests, et constater qu'ils passent : VERT
- Remanier le code pour éliminer toute duplication : REMANIEMENT
Il est essentiel que ce cycle se réalise très rapidement, en quelques minutes tout au plus. Si la réalisation du cycle prend des dizaines de minutes, il est probable que vous soyez en train d'essayer de réaliser un pas trop important ; il est alors souhaitable d'essayer d'attaquer une étape moins ambitieuse. Comme nous le verrons, la particularité du TDD est de réaliser des étapes qui peuvent paraître minuscules à des développeurs chevronnés, certains parlent même de micro-incréments de code.
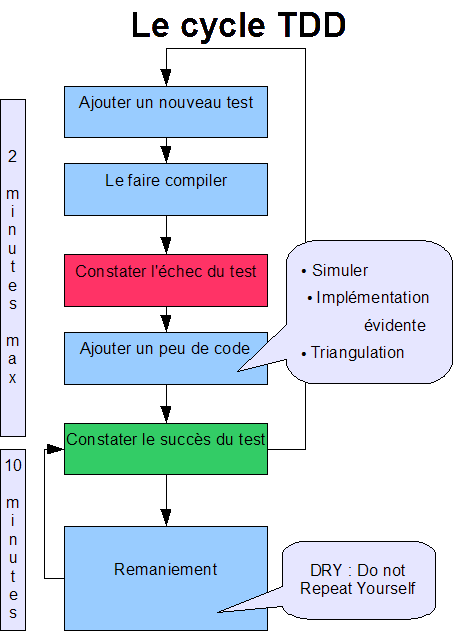
Le cycle complet est résumé par le diagramme ci-dessous, avec l'ordre de grandeur du temps à consacrer à chaque phase.
III. Premiers pas▲
III-A. Mise en place du projet▲
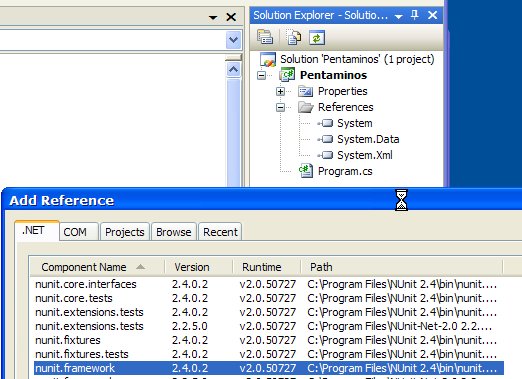
Après avoir téléchargé et installé Visual C# Express et Nunit, nous créons une application console (Menu Fichier, Nouveau Projet, et Application Console) appelées Pentaminos. Ensuite il faut ajouter la référence Nunit-framework au projet, depuis l'explorateur de solution Visual C# :
Sauvegarder la solution (menu Fichier, Sauver Tous) puis la construire (F6).
Lancer Nunit GUI, puis ouvrir l'executable produit par Visual C#, il se trouvera dans Pentaminos\bin\Release\Pentaminos.exe. Nunit GUI affiche alors notre projet, avec aucun test pour l'instant :
A partir de là nous allons passer constamment de Visual C# à Nunit : après de petites modifications dans le code C# (et reconstruction de la solution par F6) nous passerons dans Nunit GUI pour appuyer sur le bouton Run, et examiner la couleur de la barre de progression située en dessous de Run.
III-B. Premier test▲
Afin de vérifier le fonctionnement de nos outils, ajoutons un test élémentaire. Il s'agit de vérifier que le programme peut retourner une description. Les principes du TDD nous imposent d'écrire le test d'abord. Donc nous ajoutons dans le fichier Program.cs le code suivant :
[TestFixture]
public class TestProgram
{
[Test]
public void TestDescription()
{
Assert.That(Program.Description.Length, Is.GreaterThan(0));
}
}- l'attribut TestFixture, qui permet d'indiquer qu'une classe est une classe de test, et qu'elle sera visible par Nunit
- l'attribut Test, qui permet d'indiquer qu'une méthode d'une classe de test est un test. Chacune de ces méthodes est exécutée de manière complètement indépendante: en effet, Nunit va créer une nouvelle instance de la classe de test pour exécuter chacune des méthodes de tests.
- Une assertion, sous la forme Assert.That( , ). Dans ce tutoriel nous utilisons une forme très récente de ces assertions, introduite dans Nunit 2.4. Celle nouvelle forme est plus lisible et plus évolutive que la forme dite classique, dans laquelle l'assertion aurait pris la forme :
Assert.Greater(Program.Description.Length,0) ;Et il faut également insérer les déclarations suivantes au début du fichier :
using Nunit.Framework;
using Nunit.Framework.Constraints;
using Nunit.Framework.SyntaxHelpers;A ce stade, notre code ne compile pas, ce qui est prévisible. Il faut ajouter une propriété description à la classe Program :
static public string Description
{
get { return ""; }
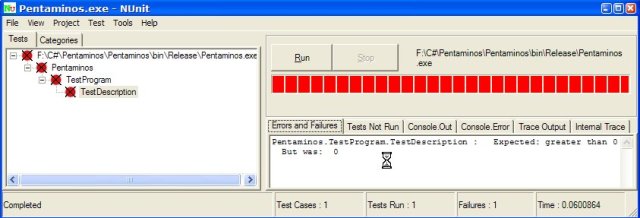
}C'est le minimum que nous pouvons faire pour pouvoir compiler. Nunit peut alors nous montrer l'exécution de ce test, qui bien sûr échoue, et donc la barre est ROUGE :
Observez également que Nunit donne des informations intéressantes sur la cause de l'échec du test.
Le minimum pour faire passer le test est de retourner la valeur attendue :
get { return "Pentaminos"; }La barre Nunit devient alors verte.
La dernière étape du cycle TDD nous impose de supprimer toute duplication de code ; il n'y en a pas ici, donc nous avons fini le cycle.
- vérifier le fonctionnement de nos outils
- observer un cycle complet de TDD : compilation, barre ROUGE, barre VERTE, remaniement du code
III-C. Notre liste de travail initiale▲
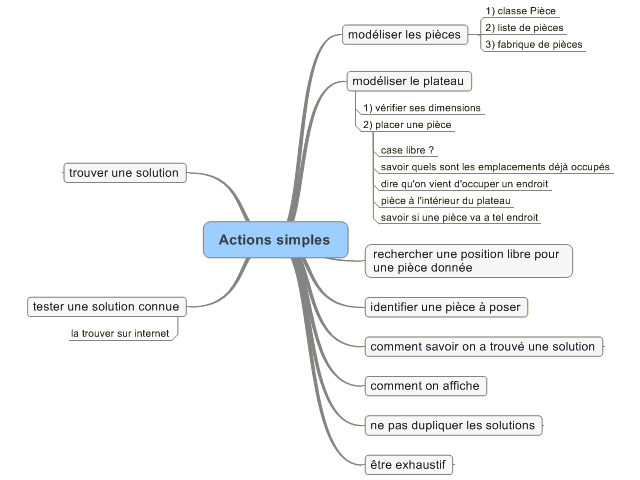
A ce stade, nous ne savons pas nécessairement comment programmer la recherche des solutions, mais cela ne doit pas nous bloquer. En effet Kent Beck recommande de mettre une point une liste de toutes les actions de programmation simples et pertinentes que nous pouvons imaginer pour progresser sur ce projet. Voici une liste de départ élaborée en quelques minutes de réflexion :
Ici nous avons utilisé un format particulier (une "mind map"), mais n'importe quel support peut être utilisé, à commencer par le papier ou un tableau blanc.
Partant de cette liste, nous pouvons commencer à travailler en TDD sur l'action qui nous paraît la plus élémentaire possible (rappelez-vous que nous allons chercher à faire des micro-incréments de code). Commençons par la modélisation des pentaminos.
IV. Modélisation des pentaminos▲
En tenant compte de toutes les rotations et symétries possibles, les 12 pentaminos peuvent présenter en tout 63 variantes. Nous allons simplement réutiliser une modélisation de ces pentaminos déjà faite par David Eck (avec sa permission), sous la forme suivante :
{
{ 1, 1,2,3,4 }, // This array represents everything the program
{ 1, 10,20,30,40 }, // knows about the individual pentominos. Each
{ 2, 9,10,11,20 }, // row in the array represents a particular
{ 3, 1,10,19,20 }, // pentomino in a particular orientation. Different
{ 3, 10,11,12,22 }, // orientations are obtained by rotating or flipping
{ 3, 1,11,21,22 }, // the pentomino over. Note that the program must
{ 3, 8,9,10,18 }, // try each pentomino in each possible orientation,
{ 4, 10,20,21,22 }, // but must be careful not to reuse a piece if
{ 4, 1,2,10,20 }, // it has already been used on the board in a
{ 4, 10,18,19,20 }, // different orientation.
{ 4, 1,2,12,22 }, // The pentominoes are numbered from 1 to 12.
{ 5, 1,2,11,21 }, // The first number on each row here tells which pentomino
{ 5, 8,9,10,20 }, // that line represents. Note that there can be
{ 5, 10,19,20,21 }, // up to 8 different rows for each pentomino.
{ 5, 10,11,12,20 }, // some pentominos have fewer rows because they are
{ 6, 10,11,21,22 }, // symmetric. For example, the pentomino that looks
{ 6, 9,10,18,19 }, // like:
{ 6, 1,11,12,22 }, // GGG
{ 6, 1,9,10,19 }, // G G
{ 7, 1,2,10,12 }, //
{ 7, 1,11,20,21 }, // can be rotated into three additional positions,
{ 7, 2,10,11,12 }, // but flipping it over will give nothing new.
{ 7, 1,10,20,21 }, // So, it has only 4 rows in the array.
{ 8, 10,11,12,13 }, // The four remaining entries in the array
{ 8, 10,20,29,30 }, // describe the given piece in the given orientation,
{ 8, 1,2,3,13 }, // in a way convenient for placing the piece into
{ 8, 1,10,20,30 }, // the one-dimensional array that represents the
{ 8, 1,11,21,31 }, // board. As an example, consider the row
{ 8, 1,2,3,10 }, //
{ 8, 10,20,30,31 }, // { 7, 1,2,10,19 }
{ 8, 7,8,9,10 }, //
{ 9, 1,8,9,10 }, // If this piece is placed on the board so that
{ 9, 10,11,21,31 }, // its topmost/leftmost square fills position
{ 9, 1,2,9,10 }, // p in the array, then the other four squares
{ 9, 10,20,21,31 }, // will be at positions p+1, p+2, p+10, and p+19.
{ 9, 1,11,12,13 }, // To see whether the piece can be played at that
{ 9, 10,19,20,29 }, // position, it suffices to check whether any of
{ 9, 1,2,12,13 }, // these five squares are filled.
{ 9, 9,10,19,29 },
{ 10, 8,9,10,11 },
{ 10, 9,10,20,30 },
{ 10, 1,2,3,11 },
{ 10, 10,20,21,30 },
{ 10, 1,2,3,12 },
{ 10, 10,11,20,30 },
{ 10, 9,10,11,12 },
{ 10, 10,19,20,30 },
{ 11, 9,10,11,21 },
{ 11, 1,9,10,20 },
{ 11, 10,11,12,21 },
{ 11, 10,11,19,20 },
{ 11, 8,9,10,19},
{ 11, 1,11,12,21 },
{ 11, 9,10,11,19 },
{ 11, 9,10,20,21 },
{ 12, 1,10,11,21 },
{ 12, 1,2,10,11 },
{ 12, 10,11,20,21 },
{ 12, 1,9,10,11 },
{ 12, 1,10,11,12 },
{ 12, 9,10,19,20 },
{ 12, 1,2,11,12 },
{ 12, 1,10,11,20 }
};
// by: David J. Eck
// Deparment of Mathematics and Computer Science
// Hobart and William Smith Colleges
// Geneva, NY 14456
// Email: eck@hws.edu
//Toutefois, le TDD nous interdit d'écrire du code avant d'avoir un test. Quel test écrire ici ? Eh bien nous pourrions vérifier qu'il y a bien 63 éléments en tout (une erreur de copier/coller est toujours possible). Donc le test pourrait être
Assert.That(ListeDePentaminos().Count, Is.EqualTo(63));En fait il faut que cette liste soit portée par une classe, donc nous choisissons d'introduire une classe FabriqueDePentaminos comme ci-dessous:
Assert.That(FabriqueDePentaminos.ListeDePentaminos().Count, Is.EqualTo(63));Le test étant défini, nous avons maintenant la permission d'écrire du code : ajoutons un fichier Pentaminos.cs au projet, fichier qui contiendra la classe de test
[TestFixture]
public class TestListePentaminos
{
[Test]
public void TestTotalPentaminos()
{
Assert.That(FabriqueDePentaminos.ListeDePentaminos().Count, Is.EqualTo(63));
}
}ainsi que tout ce qui concernera la définition des pentaminos et de leur fabrique.
Voici le code minimum pour parvenir à compiler, et passer à la barre ROUGE :
class Pentamino
{
}
class FabriqueDePentaminos
{
static public List<Pentamino> ListeDePentaminos()
{
return new List<Pentamino>();
}
}Pour avoir la barre verte, on peut écrire le code suivant :
static public List<Pentamino> ListeDePentaminos()
{
List<Pentamino> liste = new List<Pentamino>();
for (int i = 0; i < 63; i++)
{
liste.Add(new Pentamino());
}
return liste;
}Attention, 63 est dupliqué ! La troisième phase du cycle nous impose de supprimer toute duplication, ce que nous pouvons faire en introduisant une constante portée par FabriqueDePentaminos :
public const int NombreDeVariantes = 63;Le test suivant va nous forcer à remplir effectivement la structure de Pentomino. Par exemple, vérifions que le 3ème élément de la liste est bien le pentamino X, si nous avons bien compris la modélisation ; le test est alors :
[Test]
public void TestPositionDuPentominoX()
{
Pentamino x = FabriqueDePentaminos.ListeDePentaminos()[2] ;
Assert.That(x.Decalage[0], Is.EqualTo(9),
"le premier décalage de X est incorrect");
Assert.That(x.Decalage[1], Is.EqualTo(10),
"le deuxième décalage de X est incorrect");
Assert.That(x.Decalage[2], Is.EqualTo(11),
"le troisième décalage de X est incorrect");
Assert.That(x.Decalage[3], Is.EqualTo(20),
"le quatrième décalage de X est incorrect");
Assert.That(x.Variante, Is.EqualTo(2),
"la Variante de X est incorrecte");
}- en cas d'échec, il est plus difficile d'identifier quel test a échoué
- le test s'arrête dès que l'une des assertions échoue, ce qui nous prive d'informations complémentaires sur le code qui est testé ; en pratique, dans des cas plus compliqués, nous serons souvent obligés de commenter l'assertion qui a échoué, afin de voir si les autres assertions passent ou pas.
Ici nous choisissons tout de même grouper ces 5 assertions dans un seul test, et nous rendons plus évident le test qui échouera en mettant une chaîne de caractères dans l'assertion.
Ce test nous conduit à définir l'interface de Pentamino comme suit :
public int[] Decalage = new int[4];
public int Variante;ce qui nous permet d'arriver à la barre rouge. Pour avoir la barre verte, il faut maintenant remplir les pentaminos avec leur description, donc :
- ajouter un constructeur,
- insérer un tableau à deux dimensions qui contiendra la description interne des pentaminos (celle obtenue de D. Eck)
- parcourir ce tableau dans la méthode ListeDePentaminos
Ces portions ne code ne sont pas reproduites ici, voir directement le fichier source Pentamino.cs.
On peut alors remarquer qu'il est possible de remplacer la constante 63 par la dimension du tableau interne, de la manière suivante :
static public int NombreDeVariantes
{
get { return DescriptionsInternes.GetUpperBound(0) + 1; }
}- ce changement peut être fait en toute sécurité, car les tests passent toujours tous
- nous avons éliminé une autre duplication, moins évidente. Plus tard s'il faut modifier le nombre de variantes de pentaminos, il suffirait d'agir à un seul endroit, le tableau des descriptions internes.
A ce stade nous avons une première modélisation des pentaminos, couverte par deux tests qui sont présentés ci-dessous :
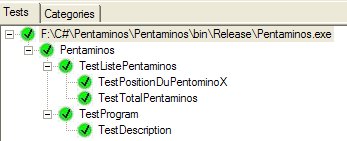
Et nous pouvons avancer sur le point suivant, la modélisation du plateau qui accueillera les pentaminos.
V. Modélisation du plateau▲
Il y a de nombreuses manières d'aborder ce point ; par exemple il est tentant de réfléchir à la structure interne de ce plateau. Allons-nous utiliser un tableau à deux dimensions, ou bien à une dimension comme la description interne des pentaminos le suggère ? Laquelle sera la plus pratique ? La plus efficace ?
Toutefois nous devons nous laisser guider par des tests avant de coder quoi que ce soit. Imaginer de tels tests est souvent très difficile pour les débutants en TDD ; pour les aider, une autre manière de voir les tests est d'imaginer qu'ils représentent des exemples de ce que l'on veut faire. Ceci va nous conduire à définir en premier une interface (un contrat) plutôt qu'une structure interne.
- pouvoir ajouter un pentamino
- ne pas pouvoir ajouter deux fois le même pentamino
- ne pas permettre de chevauchement de pentamino
- les pentaminos ajoutés ne devront pas déborder du plateau
- savoir si une solution a été trouvée
- pouvoir enlever un pentamino
- pouvoir afficher un plateau (en mode console)
V-A. Premiers tests▲
Commençons donc par écrire un test, qui bien sûr ne compilera même pas :
Assert.That(plateau.Ajoute(I));pour traduire l'intention d'ajouter un pentamino. Pour compiler, il faut alors ajouter une nouvelle classe Plateau (et un nouveau fichier Plateau.cs au projet), et le code suivant :
class Plateau
{
public Boolean Ajoute(Pentamino pentamino)
{
return false;
}
}
[TestFixture]
public class TestPlateau
{
[Test]
public void TestAjoutPentamino()
{
Plateau plateau = new Plateau();
Pentamino I = FabriqueDePentaminos.ListeDePentaminos()[0] ;
Assert.That(plateau.Ajoute(I));
}
}Ce qui permet de compiler et d'arriver à la barre rouge. Le minimum pour arriver à la barre verte est alors de changer false en true dans la méthode Ajoute.
Ces étapes minimalistes peuvent paraître superflues. Il n'en est rien. Ces petites étapes permettent de valider l'outil de test avant d'écrire le véritable code de production. En effet sur un projet réel, qui comportera des milliers de tels petits tests, il n'y a rien de pire qu'un test qui est vert tout de suite : il peut être vert par hasard, ou par erreur de construction (la condition de l'assertion est toujours vérifiée). On peut également être en train de travailler sur un autre test que celui que l'on imagine... En d'autres termes, ce qui valide un test, ce n'est pas la barre verte, c'est l'observation du passage de la barre rouge à la barre verte.
Ayant notre barre verte, et n'ayant a priori pas introduit de duplication, il faut avoir un autre test avant d'écrire plus de code ! Tout simplement
[Test]
public void TestAjoutPentaminoSansRepetition()
{
Plateau plateau = new Plateau();
Pentamino I = FabriqueDePentaminos.ListeDePentaminos()[0];
plateau.Ajoute(I);
Assert.That(plateau.Ajoute(I), Is.False);
}Ce code compile, et donne la barre rouge comme attendu. Il introduit également des duplications dans le code de test, point à régler dès que la barre verte sera obtenue. Pour obtenir la barre verte, impossible de continuer à changer des "true" en "false" : ce cas est un exemple de triangulation, où nous sommes contraints par deux tests au moins à écrire du code (ce qui oblige à généraliser).
Ici une solution assez simple est possible, donc écrivons-là directement pour avoir la barre verte :
private Boolean[] VariantesDejaAjoutees = new Boolean[12] ;
public Boolean Ajoute(Pentamino pentamino)
{
if (VariantesDejaAjoutees[pentamino.Variante])
{
return false;
}
else
{
VariantesDejaAjoutees[pentamino.Variante] = true;
return true;
}
}Il faut maintenant passer à la duplication de code présente dans la classe de test, où les deux méthodes comportent des initialisations communes. Nunit permet de grouper ces initialisations dans une méthode Setup comme suit :
private Plateau plateau;
private Pentamino I;
[SetUp]
public void SetUp()
{
plateau = new Plateau();
I = FabriqueDePentaminos.ListeDePentaminos()[0];
}Cette méthode SetUp est automatiquement appelée par Nunit avant l'exécution de chaque test (tout comme une méthode TearDown est appelée après, afin de libérer des resources si besoin).
Cela permet de supprimer la duplication, comme d'habitude en toute sécurité puisque la barre reste verte après cette opération.
A ce stade nous avons confiance que la méthode Ajoute gérera correctement les ajouts de pentaminos sans permettre d'ajouter deux fois le même, ni deux variantes du même pentamino, donc nous n'écrivons pas plus de tests sur ce point.
Maintenant nous pouvons déjà traiter l'identification d'une solution trouvée, en considérant qu'il suffira qu'un pentamino de chaque sorte ait été posé.
Voici un premier test
[Test]
public void TestSolutionTrouveePlateauVide()
{
Assert.That(plateau.SolutionTrouvee, Is.False);
}pour compiler et passer à la barre rouge :
public Boolean SolutionTrouvee
{
get { return true; }
}- Changer true en false (barre verte) - mais cette solution ne marche pas dans tous les cas, il faut alors ajouter un test supplémentaire, du type ajouter les 12 pentaminos d'une solution connue, et vérifier la valeur de SolutionTrouvee. C'est la méthode de triangulation, qui continue à nous faire faire de tout petits pas.
- Considérer que l'implémentation est évidente, et sans risque, et faire un pas un peu plus grand.
Prenons l'implémentation évidente, afin de montrer que le développeur a le choix de la taille des pas :
public Boolean SolutionTrouvee
{
get { return (TotalVariantesDejaAjoutees == FabriqueDePentaminos.NombreDePentaminos) ; }
}- le code nécessaire à la déclaration et l'initialisation de TotalVariantesDejaAjoutees
- l'incrémentation de TotalVariantesDejaAjoutees dans la méthode Ajoute
- l'extraction d'une méthode privée Pose, afin de rendre indissociables les deux opérations qu'il faut maintenant faire quand un pentamino est ajouté. Noter que nous ne cherchons pas à tester cette méthode privée : en TDD on se contente de tester l'interface publique d'une classe, afin d'éviter que le test ne se fragilise en devenant dépendant d'une structure interne susceptible d'évoluer.
- la déclaration d'une constante NombreDePentaminos dans la fabrique de pentaminos, afin de supprimer la duplication du nombre 12.
Voici donc un pas plus important, qui n'est pas sans risque ; un débutant programmeur aurait certainement intérêt à prendre l'option a) ci-dessus.
V-B. Gestion des chevauchements▲
La barre verte est maintenant obtenue, et nous passons à la gestion des chevauchements.
- ajouter le I à un certain endroit
- vérifier qu'il n'est pas possible d'ajouter un autre pentamino, disons le X, au même endroit.
- la méthode Ajoute ne permet pas de préciser un "endroit"
- définir la notion d' "endroit" ne paraît pas possible sans se poser la question de la structure interne décrivant le plateau : il faut maintenant se décider. Étant donné que la modélisation des pentaminos suggère un tableau sous la forme d'un tableau à une dimension, prenons cette direction, quitte à changer d'avis plus tard si elle n'est pas suffisamment pratique ; le tableau ci-dessous décrit toutes ces positions :
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 |
| 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 |
| 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 |
- pour le moment il ne paraît pas judicieux de modifier la méthode Ajoute, qui comporte déjà quelques lignes de code déjà testées. Aussi nous allons plutôt partir sur une méthode VerifierPlaceLibre, qui sera testée comme suit :
Assert.That(plateau.VerifierPlaceLibre(I, 1), Is.True);Nous obtenons facilement barre rouge puis verte en retournant la constante false, puis true, et il faut alors trianguler avec un deuxième test :
plateau.Ajoute(I, 1);
Assert.That(plateau.VerifierPlaceLibre(X, 1), Is.False);Alors nous nous rendons compte qu'il faut maintenant modifier Ajoute qui a besoin d'un deuxième paramètre, ce qui implique de modifier les trois tests qui portent déjà sur Ajoute.
La barre rouge est alors obtenue, et pour avoir la barre verte, il est indispensable que le plateau mémorise de l'information quand un pentamino est posé. C'est le moment de déclarer un tableau de cases :
private Boolean[] Cases = new Boolean[60];puis le remplir lors de la pose d'un pentamino
private void Pose(Pentamino pentamino, int position)
{
VariantesDejaAjoutees[pentamino.Variante] = true;
TotalVariantesDejaAjoutees++;
Cases[position] = true;
foreach (int decalage in pentamino.Decalage)
{
Cases[position + decalage] = true;
}
}Noter que Pose reste privée, car aucun test ne porte directement sur elle.
Il est alors possible d'écrire la vérification de place libre :
public Boolean VerifierPlaceLibre(Pentamino pentamino, int position)
{
if (Cases[position])
{
return false;
}
else
{
Boolean toutes_libres = true;
foreach (int decalage in pentamino.Decalage)
{
toutes_libres = Cases[position + decalage];
if (!toutes_libres)
{
break;
}
}
return toutes_libres;
}
}Toutefois, le premier test sur VerifierPlaceLibre ne passe pas, alors que le deuxième passe ! Après examen du code, il y erreur sur le calcul de toutes_libres, qui doit être
toutes_libres = !Cases[position + decalage];Ici nous voyons l'intérêt d'avoir triangulé ce test, et nous voyons aussi l'intérêt des tests unitaires, qui capturent au plus tôt ce type d'erreur de programmation très fréquente.
La barre verte est alors obtenue. En examinant les possibles duplications, nous pouvons remarquer que deux fois nous avons une gestion de Cases[position] suivie d'un foreach sur les décalages, ce qui introduit un risque car il faut toujours penser à ces deux situations. Si l'on introduit artificiellement un décalage supplémentaire de zéro dans le tableau décrivant les décalages, ce problème disparaîtrait. Modifions donc la classe Pentamino comme suit :
public int[] Decalage = new int[5];
public int Variante;
public Pentamino(int variante, int decalage1, int decalage2, int decalage3, int decalage4)
{
Variante = variante;
Decalage[0] = decalage1;
Decalage[1] = decalage2;
Decalage[2] = decalage3;
Decalage[3] = decalage4;
Decalage[4] = 0;
}Le décalage de zéro est introduit en dernier afin de ne pas casser les tests existants. Au passage on peut noter le grand intérêt de foreach qui nous évite bien des risques de duplications de taille de tableau qu'il faudrait sinon gérer avec des constantes.
Après avoir vérifié que tous les tests passent encore, nous pouvons modifier Pose et VerifierPlaceLibre :
public Boolean VerifierPlaceLibre(Pentamino pentamino, int position)
{
Boolean toutes_libres = true;
foreach (int decalage in pentamino.Decalage)
{
toutes_libres = !Cases[position + decalage];
if (!toutes_libres)
{
break;
}
}
return toutes_libres;
}Nous avons donc supprimé une duplication, et simplifié deux fonctions. Les tests passent toujours après cette opération, donc nous avons une certaine confiance dans nos travaux. En raffinant encore un peu il est possible d'éliminer toutes_libres ci-dessus :
public Boolean VerifierPlaceLibre(Pentamino pentamino, int position)
{
foreach (int decalage in pentamino.Decalage)
{
if (Cases[position + decalage])
{
return false;
}
}
return true;
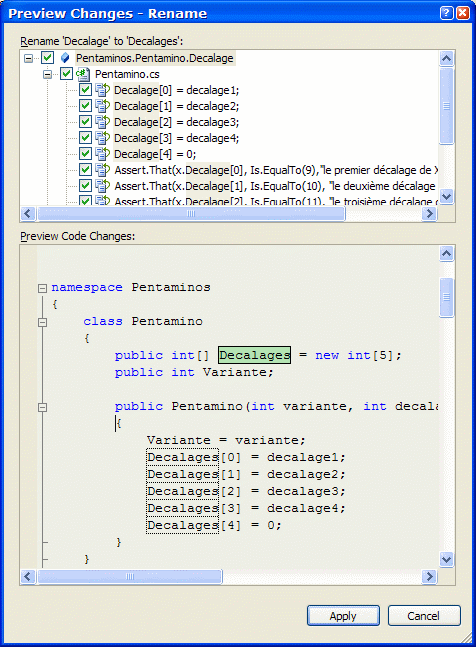
}Ce qui est finalement plus lisible. Enfin, il serait aussi plus lisible de passer Decalage au pluriel (pentamino.Decalages), que Visual Studio peut remplacer facilement à travers toute la solution avec l'outil Refactor/Rename :
Encore une fois, même si ce renommage est trivial, disposer de tests unitaires nous permet de remanier le code en toute sécurité. Ceci est d'autant plus vital que les environnements de développement proposent des outils de remaniement de plus en plus perfectionnés (le Rename ci-dessus en étant l'illustration la plus basique). Pratiquer le TDD est donc un moyen de mieux tirer parti de ces nouveaux outils.
Écrivons encore un test sur VerifierPlaceLibre :
Assert.That(plateau.VerifierPlaceLibre(I, 9), Is.False);En effet le pentamino I horizontal ne doit pas pouvoir être posé à la fin de la première ligne, car il déborderait du plateau. Nous obtenons logiquement la barre rouge, car aucune précaution n'a été prise pour l'instant contre cette situation.
Pour arriver rapidement à la barre verte, nous pouvons ajouter artificiellement des cases au tableau, afin de bloquer les possibilités de débordement (ces cases sont souvent appelées des sentinelles) :

(les pentaminos étant toujours décrits par leur position la plus "haute", il n'y pas de débordement possible par le haut du tableau)
Nous avons alors un tableau de 84 cases qu'il faut initialiser soigneusement dans un constructeur de la classe Plateau :
public Plateau()
{
int position = 0;
for (int index_ligne = 1; index_ligne <= 6; index_ligne++)
{
Cases[position++] = true;
for (int index_colonne = 1; index_colonne <= 10; index_colonne++)
{
Cases[position++] = false;
}
Cases[position++] = true;
}
for (int index_colonne = 0; index_colonne <= 11; index_colonne++)
{
Cases[position++] = true;
}
}Cela suffit effectivement à faire passer le test. La suppression des duplications nous impose de factoriser les dimensions du tableau (6, 10, 11) - que nous faisons avec des constantes dans la classe Plateau.
Le constructeur de Plateau est assez complexe, avec plusieurs boucles, et des erreurs possibles sur leurs bornes. Il est donc important d'ajouter des tests complémentaires.
Par exemple le X ne doit pas pouvoir être mis en 37 ni 65, mais il doit pouvoir être mis en 45. J'ajoute donc ces trois tests, chacun avec sa méthode (plutôt que de mettre trois assertions dans une seule méthode). Ces trois tests passent, ce qui laisse penser que le tableau est initialisé correctement.
V-C. Utilisation d'une solution connue▲
Il serait maintenant agréable de remplir le tableau avec une solution connue, afin d'exercer tout le code déjà écrit sur un test conséquent. Il serait également pratique de pouvoir ajouter les pentaminos sans calculer à la main leur position exacte, par exemple avec une méthode ProchainePositionLibre, qui pourrait être testée comme suit :
public void ProchainePositionPlateauVide()
{
Assert.That(plateau.ProchainePositionLibre(), Is.EqualTo(1));
}La barre verte est obtenue comme d'habitude par le retour d'une constante, puis on triangule avec un test supplémentaire :
[Test]
public void ProchainePositionPlateauApresI()
{
plateau.Ajoute(I, 1);
Assert.That(plateau.ProchainePositionLibre(), Is.EqualTo(6));
}Ce qui permet l'implémentation de la fonction :
public int ProchainePositionLibre()
{
while (Cases[PositionLibreActuelle])
{
PositionLibreActuelle++;
}
return PositionLibreActuelle;
}Aucune boucle infinie n'est à craindre grâce aux sentinelles.
Pour travailler sur l'exemple d'une solution connue, ajoutons une nouvelle "TestFixture", disons TestSolutionConnue, puis écrivons le code de test :
public void ConstructionSolutionComplete()
{
foreach (int i in SolutionIndexes)
{
Assert.That(plateau.Ajoute(liste[i],plateau.ProchainePositionLibre()),
Is.True, "échec du test numéro " + i.ToString()) ;
}
}Mais la barre rouge est obtenue avec l'affichage du problème suivant :
Pentaminos.TestPlateauAvecSolutionConnue.ConstructionSolutionComplete :
System.IndexOutOfRangeException : Index was outside the bounds of the array.
at Pentaminos.Plateau.Ajoute(Pentamino pentamino, Int32
position) in F:\C#\Pentaminos\Pentaminos\Plateau.cs:line 52
at Pentaminos.TestPlateauAvecSolutionConnue.ConstructionSolutionCom
plete() in F:\C#\Pentaminos\Pentaminos\Plateau.cs:line 212Il y a donc un problème dans la méthode Ajoute. La ligne en question est
if (VariantesDejaAjoutees[pentamino.Variante])et on peut supposer un problème de dimension du tableau VariantesDejaAjoutees. Il est alors prudent d'ajouter un nouveau test spécifique pour reproduire ce problème, car nos tests précédents sont visiblement insuffisants :
[Test]
public void DepassementLimites()
{
Assert.That(plateau.Ajoute(FabriqueDePentaminos.ListeDePentaminos()[62], 27));
}Ce test confirme bien le problème, on remarque alors que les variantes vont de 1 à 12, alors que le tableau va de 0 à 11. Pour faire le minimum de corrections, il faut intervenir dans le constructeur de Pentamino, et soustraire 1 à chaque variante. La barre passe alors au vert pour tous les tests, sauf l'un des plus anciens :
Pentaminos.TestListePentaminos.TestPositionDuPentominoX : la variante de X est incorrecte
Expected: 2
But was: 1Après correction de cet ancien test, la barre est enfin verte ! Ce petit incident nous ayant rendu méfiants par rapport au code déjà écrit, ajoutons un test complémentaire sur SolutionTrouvee, qui est facile maintenant que nous avons une solution complète :
Assert.That(plateau.SolutionTrouvee, Is.False);Pour se forcer à constater la barre rouge, puis bien sûr :
Assert.That(plateau.SolutionTrouvee, Is.True);V-D. Principe de l'algorithme▲
Nous disposons de pratiquement toutes les briques de bases pour un algorithme de recherche de toutes les solutions, du type
Fonction recursive ChercheSolutions(plateau ; liste de pentaminos)
Si plateau.SolutionTrouvee Alors
plateau.AfficherSolution
Sinon
position = plateau.ProchainePositionLibre()
Pour chaque pentamino P dans la liste
Si plateau.Ajoute(P, position) Alors
ChercheSolutions(plateau, liste de pentaminos)
Plateau.Enleve(P,position)
FinSi
FinSiC'est un algorithme classique de retour en arrière. Si l'on n'a pas encore rencontré ce type d'algorithme, il n'est pas très facile de découvrir cet algorithme en se laissant simplement guider par le TDD, et il semble que l'on rencontre ici une limite de cette démarche du TDD. Toutefois le TDD promet simplement du "code propre qui fonctionne", il ne promet pas la découverte d'algorithmes astucieux.
V-E. Dernières briques▲
- l'affichage en mode console d'une solution
- enlever un pentamino
Commençons par l'affichage. Les possibilités en mode console sont limitées, et une façon simple de procéder serait de décrire chaque pentamino par sa lettre X, I dans chaque case du tableau.
Quel test écrire ? Une première idée consiste à tester une chaîne de caractères fournie par le plateau, et à vérifier qu'elle est égale à la chaîne de 60 caractères attendue. En pratique, en cas d'erreur, il est difficile de localiser quels caractères sont faux. On peut aussi tester individuellement chaque caractère. Enfin une troisième idée consiste à faire retourner par le plateau 6 chaînes de 10 caractères, que l'on testera séparément. Cela est suffisant pour identifier des erreurs, et d'autre part le test couvrira également le découpage en lignes pour l'affichage en mode console.
Commençons par ajouter un test dans la TestFixture TestSolutionConnue :
[Test]
public void DescriptionLigne1()
{
Assert.That(plateau.Lignes()[0], Is.EqualTo("VVVTTTWWFF"));
}Une petite difficulté se présente… Pour ce test nous avons besoin du code de construction de la solution, qui est pour le moment présent uniquement dans le test précédent. Le dupliquer n'est pas acceptable en TDD, donc il nous faut trouver un moyen de le factoriser dans la méthode Setup :
private string ResultatsMethodeAjoute = "";
private string ResultatsAttendus = "";
[SetUp]
public void SetUp()
{
plateau = new Plateau();
foreach (int i in SolutionIndexes)
{
ResultatsMethodeAjoute += plateau.Ajoute(liste[i],
plateau.ProchainePositionLibre()).ToString() + " ";
ResultatsAttendus += false.ToString() + " ";
}
}Cette technique permet de forcer le test à nous donner le maximum de résultats, au contraire de la construction précédente avec foreach : le test s'arrête au premier échec. Tandis qu'ici nous obtenons plus d'informations :
Pentaminos.TestPlateauAvecSolutionConnue.ConstructionSolutionComplete :
Expected string length 72 but was 60. Strings differ at index 0.
Expected: "False False False False False False False False False False F..."
But was: "True True True True True True True True True True True True "Pour obtenir la barre verte il faut alors remplace false par true dans la construction des résultats attendus.
Ayant factorisé ce code, il devient facile d'isoler le test sur SolutionTrouve, ce qui résout un point insatisfaisant mentionné plus haut. Nous pouvons maintenant revenir à DescriptionLigne1, que nous avions commenté en attendant.
Ici nous rencontrons une limite : les cases contiennent des booléens, qui avaient paru un choix naturel lors de l'écriture des tests précédents, pas les caractères qui seraient maintenant beaucoup plus pratiques. Aucun problème toutefois : changeons le type du tableau Cases en char, et à l'aide du compilateur et de l'exécution des tests unitaires, implémentons tous les changements nécessaires jusqu'à obtenir à nouveau la barre verte :
- premier changement : guidé par un nouveau test
Assert.That(x.Representation, Is.EqualTo('X'), "X n'est pas représenté par la bonne lettre");nous pouvons modifier la classe Pentamino et la fabrique de pentamino pour gérer les représentations des pentaminos sous forme de lettre
- deuxième changement : pour arriver à compiler, il faut à plusieurs endroits remplacer affectations et comparaisons grâce à deux constantes de la classe Plateau :
private const char POSITIONINTERDITE = '.';
private const char POSITIONLIBRE = ' ';- dernier changement : modifier la méthode Pose pour stocker la représentation de chaque pentamino.
Tous les tests passent alors, à l'exception de notre dernier test sur les lignes. Le code suivant permet de le faire passer :
public List<string> Lignes()
{
List<string> liste = new List<string>();
string ligne_en_cours = "";
foreach (char c in Cases)
{
if (c != POSITIONINTERDITE)
{
ligne_en_cours += c;
}
if (ligne_en_cours.Length == NOMBRE_DE_COLONNES)
{
liste.Add(ligne_en_cours);
ligne_en_cours = "";
}
}
return liste;
}Nous pouvons alors tester la deuxième ligne :
Assert.That(ListeLignes[1], Is.EqualTo("VUUUTWWFFL"));Et surprise, le test ne passe pas :
Pentaminos.TestPlateauAvecSolutionConnue.DescriptionLigne2 :
String lengths are both 10. Strings differ at index 4.
Expected: "VUUUTWWFFL"
But was: "VUUUWWFFLV"
---------------^On voit que le V n'est pas correctement placé. Il y a donc potentiellement un problème dans la méthode Ajoute, problème qui n'est pas capturé par nos tests actuels. Il faut donc imaginer un nouveau test qui reproduit cette situation. Ce test doit ajouter V, et vérifier que V occupent bien les cases attendues. Or nous n'avons pas accès à Cases qui est privée, et devrait le rester car il n'est pas souhaitable d'exposer cette structure interne. Heureusement nous pouvons tester indirectement l'occupation des cases via VerifierPlaceLibre, comme suit :
public void PlacementVenPosition1()
{
plateau.Ajoute(FabriqueDePentaminos.ListeDePentaminos()[08],1) ;
Assert.That(plateau.VerifierPlaceLibre(I, 2), Is.False);
Assert.That(plateau.VerifierPlaceLibre(I, 3), Is.False);
Assert.That(plateau.VerifierPlaceLibre(I, 4), Is.True);
Assert.That(plateau.VerifierPlaceLibre(I, 13), Is.False);
Assert.That(plateau.VerifierPlaceLibre(I, 25), Is.False);
}La cinquième assertion finit par reproduire le problème, le V n'est donc pas ajouté correctement…
Un autre test, plus direct, et donnant plus d'informations, serait d'utiliser la description des lignes, comme suit :
public void PlacementVenPosition1viaLignes()
{
plateau.Ajoute(FabriqueDePentaminos.ListeDePentaminos()[08], 1);
Assert.That(plateau.Lignes()[0],Is.EqualTo("VVV ")) ;
Assert.That(plateau.Lignes()[1],Is.EqualTo("V ")) ;
Assert.That(plateau.Lignes()[2],Is.EqualTo("V ")) ;
}Et ce test nous donne finalement la clé du mystère :
Pentaminos.TestPlateau.PlacementVenPosition1viaLignes :
String lengths are both 10. Strings differ at index 9.
Expected: "V "
But was: "V V"
--------------------^L'un des éléments du V est clairement mal positionné. En fait nous avons modifié la dimension du tableau de Cases, de 60 à 84 (donc de 7 par 12), mais sans prendre en compte les répercussions sur la modélisation des pentaminos, qui était prévue pour un tableau de 6 par 10. Il faut donc corriger les décalages, par exemple dans le constructeur de Pentamino. On peut le faire soit directement (implémentation évidente), soit en écrivant des tests supplémentaires pour tester la correction. Prenons l'implémentation évidente :
private int Correction(int decalage6x10)
{
int supplement = 0;
if (decalage6x10 >= 8)
{
supplement += 2;
}
if (decalage6x10 >= 18)
{
supplement += 2;
}
if (decalage6x10 >= 28)
{
supplement += 2;
}
if (decalage6x10 >= 38)
{
supplement += 2;
}
return decalage6x10 + supplement;
}Qui nous permet de passer tous les tests.
- ajouter un pentamino sur le plateau (vide)
- enlever ce pentamino
- vérifier qu'on peut l'ajouter à nouveau à la même position
Un autre test consisterait à vérifier qu'on peut ajouter une autre variante de ce pentamino après l'avoir enlevé.
Donc pour le premier test :
public void AjouterPuisEnleverI()
{
plateau.Ajoute(I, 1);
plateau.Enleve(I, 1);
Assert.That(plateau.Ajoute(I, 1), Is.True);
}Puis pour arriver à la barre verte, on utilise l'implémentation évidente :
public void Enleve(Pentamino pentamino, int position)
{
VariantesDejaAjoutees[pentamino.Variante] = false;
TotalVariantesDejaAjoutees--;
foreach (int decalage in pentamino.Decalages)
{
Cases[position + decalage] = POSITIONLIBRE;
}
}Les tests passent, mais nous avons du code dupliqué, car la méthode Enleve est construire sur exactement le même modèle que la méthode Pose : plus tard si nous changeons Pose, il faudra surement modifier Enlever. Le TDD nous force à supprimer cette duplication, ce qui est possible en factorisant le code commun comme suit :
private void Pose(Pentamino pentamino, int position, Boolean ajout)
{
VariantesDejaAjoutees[pentamino.Variante] = ajout;
TotalVariantesDejaAjoutees = TotalVariantesDejaAjoutees + (ajout ? 1 : -1);
foreach (int decalage in pentamino.Decalages)
{
Cases[position + decalage] =
ajout ? pentamino.Representation : POSITIONLIBRE;
}
}
public void Enleve(Pentamino pentamino, int position)
{
Pose(pentamino,position,false);
}Les tests continuent à tous passer. Ici nous avons suffisamment confiance dans notre code, en particulier grâce à la factorisation, donc nous considérons qu'il n'est pas nécessaire d'ajouter un deuxième test.
Toutefois cette méthode Enlever doit restaurer le plateau dans son état précédent, et elle doit également remettre à jour la position libre actuelle. Pour cela nous avons besoin d'un test, comme
[Test]
public void PositionLibreApresAjouterPuisEnleverI()
{
plateau.Ajoute(I, 1);
int position_libre = plateau.ProchainePositionLibre();
plateau.Enleve(I, 1);
Assert.That(plateau.ProchainePositionLibre(), Is.EqualTo(1));
}A noter que nous avons préféré ajouter un nouveau test plutôt que mettre une assertion supplémentaire dans le test déjà existant.
Remarque : la méthode Pose est un excellent endroit pour vérifier certains invariants de notre code. En effet nous ne devrions jamais être en train d'ajouter un pentamino sur une case déjà occupée par un autre pentamino, ni jamais rendre libre une case déjà libre. Mais nous ne pouvons pas utiliser les tests unitaires pour cela, car nous ne voulons pas rendre les tests dépendant des structures internes et privées. Les assertions "traditionnelles" (voir par exemple https://smeric.developpez.com/java/astuces/assertions/) sont alors très utiles, et parfaitement complémentaires des tests unitaires. La méthode Pose pourrait donc comporter l'assertion suivante :
Debug.Assert( (Cases[position + decalage] == POSITIONLIBRE) == ajout);Toutefois les assertions ne sont exécutées que dans la configuration Debug, et il faut donc ajouter également au projet Nunit l'exécutable Pentaminos\bin\Debug\Pentaminos.exe, et alors exécuter les tests sur la version Debug au lieu de la version Release
VI. Implémentation de l'algorithme▲
Nous disposons de toutes les briques de base, et elles devraient maintenant bien fonctionner étant donné notre batterie de tests.
VI-A. Un test fonctionnel▲
Comment faire pour coder cet algorithme décrit plus haut ? Faut-il un test unitaire ? Par définition les tests unitaires doivent s'exécuter très rapidement, en quelques secondes. Ici nous nous apprêtons à implémenter un algorithme qui va mettre plusieurs minutes à trouver toutes les solutions, donc nous sortons du cadre du test unitaire.
Toutefois rien ne nous empêche de réaliser un test automatisé avec Nunit - tout test devrait être aussi automatisé que possible - mais il faut être conscient que ce n'est pas un test unitaire : c'est un test fonctionnel automatisé via Nunit, à défaut d'avoir ici un outil spécialisé pour automatiser des tests fonctionnels.
Un test simple consiste à vérifier que notre algorithme calcule toutes les solutions :
[TestFixture]
[Category("Tests fonctionnels")]
public class TestAlgorithme
{
[Test]
public void NombreDeSolutions()
{
Algorithme algorithme = new Algorithme(new Plateau(), FabriqueDePentaminos.ListeDePentaminos());
Assert.That(algorithme.ChercheSolutions(), Is.EqualTo(4 * 2339));
}
}Afin de le distinguer clairement des autres tests, nous avons utilisé l'attribut Category fourni par Nunit, qui permet d'enrichir la classe de test. Par souci d'homogénéité, nous avons rangé tous les autres tests déjà écrits dans la catégorie Tests unitaires. Nunit permet alors facilement de jouer les tests d'une catégorie particulière (voir les figures ci-dessous) :

Nous pouvons alors coder l'algorithme (dans un nouveau fichier Algorithme.cs) :
public int ChercheSolutions()
{
if (Plateau.SolutionTrouvee)
{
Plateau.Affiche();
return 1;
}
else
{
int total_solutions = 0;
int position_libre = Plateau.ProchainePositionLibre();
foreach (Pentamino pentamino in Liste)
{
if (Plateau.Ajoute(pentamino, position_libre))
{
total_solutions += ChercheSolutions();
Plateau.Enleve(pentamino, position_libre);
}
}
return total_solutions;
}
}Malheureusement malgré toutes nos précautions précédentes, ce test échoue:
Pentaminos.TestAlgorithme.NombreDeSolutions : Expected: 9356
But was: 8787A ce stade, il n'y a guère d'autre solution que d'afficher les diverses solutions, afin de tenter de remarquer quelque chose d'anormal. Heureusement, dès la deuxième solution, nous voyons que le pentamino L est mal formé:
IIIIIXZZPP
YYYYXXXZPP
FYNNNXTZZP
FFFWNNTVVV
UFUWWTTTLV
UUULWWLLLVAfin de mettre ce problème en évidence sur un cas élémentaire, écrivons un test supplémentaire:
[Test]
public void PlacementLenPosition5viaLignes()
{
plateau.Ajoute(FabriqueDePentaminos.ListeDePentaminos()[30],5) ;
Assert.That(plateau.Lignes()[0], Is.EqualTo(" L "));
Assert.That(plateau.Lignes()[0], Is.EqualTo(" LLLL "));
}Ce test échoue comme prévu. La recherche du L correspondant a d'autre part mis en évidence que l'un des décalages est 7, qui n'est pas correctement prévu par notre fonction Correction. La solution consiste donc à corriger cette fonction. Tous les tests passent alors, et nous avons toutes les solutions.
Nous pouvons alors écrire le code d'appel dans le programme, afin de pouvoir exécuter notre algorithme sans Nunit:
static void Main(string[] args)
{
Algorithme algorithme = new Algorithme(new Plateau(), FabriqueDePentaminos.ListeDePentaminos());
int total_solutions = algorithme.ChercheSolutions();
Console.WriteLine("Nombre total de solutions : {0} ", total_solutions);
}VI-B. Perfectionnements▲
VI-B-1. Réduction du nombre de solutions▲
Il est possible de se limiter au calcul des 2239 solutions en forçant le pentamino X à rester dans le premier quadrant du plateau : en effet, si une certaine solution est obtenue avec le X dans le premier quadrant, en faisant 3 symétries on obtient directement 3 autres solutions.
Comme toujours, écrivons un test (fonctionnel ici) :
[Test]
public void NombreDeSolutionsUniques()
{
Algorithme algorithme = new AlgorithmeSansSymetries(new Plateau(),
FabriqueDePentaminos.ListeDePentaminos());
Assert.That(algorithme.ChercheSolutions(), Is.EqualTo(NombreSolutionsUniques));
}Nous avons factorisé le nombre de solutions dans un champs privé de la classe de tests, afin de respecter le principe DRY même dans les classes de tests.
Le test ci-dessus montre que au lieu d'ajouter une option à l'algorithme, nous avons introduit une nouvelle classe d'algorithme. Le principe des deux algorithmes étant très proche, nous allons utiliser le patron de conception "Template" pour permettre aux classes dérivées de Algorithme d'implémenter la possibilité de rejeter certaines pièces à certaines positions. Pour cela il suffit de modifier la tentative d'ajout de pentamino comme suit:
if (Accepte(pentamino,position_libre) && (Plateau.Ajoute(pentamino, position_libre)))où Accepte est une fonction virtuelle que les classes dérivées pourront redéfinir:
virtual protected Boolean Accepte(Pentamino pentamino, int position)
{
return true;
}Puis nous pouvons implémenter la classe dérivée. Tout d'abord nous visons à compiler et obtenir la barre rouge :
class AlgorithmeSansSymetries : Algorithme
{
public AlgorithmeSansSymetries(Plateau plateau, List<Pentamino> liste)
: base(plateau, liste)
{
}
protected override bool Accepte(Pentamino pentamino, int position)
{
return false;
}
}le test s'exécute très rapidement étant donné que tous les pentaminos sont rejetés ! Pour passer à la barre verte nous pouvons écrire directement l'implémentation évidente:
static private Boolean EstDansIntervalle(int x, int a, int b)
{
return (x >= a) && ( x<= b) ;
}
protected override bool Accepte(Pentamino pentamino, int position)
{
if (pentamino.Variante == 1)
{
return (EstDansIntervalle(position, 1, 5) ||
EstDansIntervalle(position, 13, 17));
}
else
{
return true;
}
}Le test (fonctionnel) passe alors au vert, mais cela prend beaucoup de temps. Afin de terminer le cycle, regardons les duplications. Il y en a, car les les nombres 5, 13, 17, ainsi que le nombre d'intervalles dépendent des dimensions du tableau. Changer les dimensions du tableau rendrait ces nombres invalides. Il faut donc les obtenir à partir des dimensions du tableau.
Ici l'implémentation évidente sert simplement d'appui intermédiaire avant de passer à une généralisation un peu plus difficile. Le plus simple semble de raisonner en termes de coordonnées (x,y), ce qui implique d'utiliser correctement les opérateurs modulo et division entière. Par expérience, ces opérateurs sont souvent utilisés en tâtonnant... Il est donc souhaitable de s'appuyer sur des tests unitaires appropriés, comme :
[Test]
public void TestConversionPosition1()
{
int x, y;
(new Plateau()).CoordonnesXY(1, out x, out y);
Assert.That(x,Is.EqualTo(0), "coordonnée x incorrecte") ;
Assert.That(y, Is.EqualTo(1), "coordonnée y incorrecte");
}Nous avons donc considéré que la conversion était un service que devait offrir le plateau (en effet il connaît ses dimensions, donc il dispose des informations nécessaires). Le code suivant donne la barre rouge :
public void CoordonnesXY(int position, out int x, out int y)
{
x = 0;
y = 0;
}Il est alors prudent de trianguler, après avoir obtenu la barre verte grâce à l'implémentation évidente (retourner (0,1) au lieu de (0,0)). Un deuxième test peut porter sur la position 27 par exemple, avec comme résultat attendu (2,3), ce qui nous permet de généraliser comme suit :
public void CoordonnesXY(int position, out int x, out int y)
{
x = position / (NOMBRE_DE_COLONNES + 2);
y = position % (NOMBRE_DE_COLONNES + 2);
}Nous pouvons alors revenir au problème en cours, à savoir la généralisation de la fonction Accepte : il va falloir comparer les coordonnées (x,y) avec les dimensions du tableau. Or celles-ci sont privées pour l'instant, il faudrait les rendre publiques. Pourquoi ne pas plutôt laisser le plateau déterminer lui-même si une position est dans son premier cadran? A ce moment-là la fonction CoordonneesXY n'a plus de raison d'être publique, à part pour être utilisée dans les tests. C'est un cas où il faut accepter de supprimer les tests que nous venons d'écrire : nous venons de trouver une meilleure interface (meilleure dans le sens où elle encapsule plus de détails d'implémentation à l'intérieur de la classe Plateau). De toute manière, les deux tests que nous supprimons sont rendus obsolètes par un test équivalent sur la future nouvelle fonction publique :
[Test]
public void TestPosition27DansPremierQuadrant()
{
Assert.That((new Plateau()).EstDansPremierQuadrant(27), Is.False);
}ce qui permettra d'arriver, après quelques étapes que nous n'indiquons pas, à la nouvelle version de Accepte :
protected override bool Accepte(Pentamino pentamino, int position)
{
if (pentamino.Variante == 1)
{
return Plateau.EstDansPremierQuadrant(position) ;
}
else
{
return true;
}
}Cette nouvelle interface à conduit à l'écriture d'un test plus simple, ce qui est généralement le signe d'une bonne évolution de l'interface.
Cette façon de procéder est assez courante quand nous nous servons du TDD pour mettre au point des méthodes privées un peu délicates :
- faire passer des tests sur une méthode temporairement publique A
- faire passer des tests sur une méthode réellement publique B, qui utilise A
- rendre A privée
- supprimer les tests qui portaient sur A
Cela peut sembler une perte de temps, mais il n'en est rien : il n'est pas rare de voir des développeurs tâtonner sur la bonne utilisation de la division entière plus longtemps que les quelques minutes qu'il a fallu pour écrire et supprimer ces tests intermédiaires.
VI-B-2. Autres dimensions de plateaux▲
Tout au long du tutoriel nous avons essayé d'appliquer le principe DRY (Do Not Repeat Yourself) qui est un principe essentiel de la programmation professionnelle. Une vérification ultime serait de pouvoir adapter facilement notre travail à d'autres dimensions de plateaux.
Comme d'habitude tout commence par un test : nous pouvons vérifier que nous trouvons bien le même nombre de solutions pour un plateau de de 10 lignes par 6 colonnes que pour un plateau de 6 lignes par 10 colonnes :
[Test]
public void EchangeDeDimensions()
{
Algorithme algorithme = new Algorithme(new Plateau(10,6),
FabriqueDePentaminos.ListeDePentaminos());
Assert.That(algorithme.ChercheSolutions(), Is.EqualTo(4 * NombreSolutionsUniques));
}Pour compiler, il suffit d'ajouter un nouveau constructeur à la classe Plateau ; nous choisissons cette solution afin de ne pas retoucher tous les tests existants (préservation de l'interface existante) :
public Plateau(int nombreLignes, int nombreColonnes)
{
}
public Plateau()
{
... initialisations
}La barre rouge est obtenue, car le reste de l'initialisation du premier constructeur est manquante. Nous partons alors sur l'implémentation évidente, qui est de factoriser ce code d'initialisation.
public Plateau(int nombreLignes, int nombreColonnes)
{
NOMBRE_DE_LIGNES = nombreLignes;
NOMBRE_DE_COLONNES = nombreColonnes;
Cases = new Char[(NOMBRE_DE_COLONNES + 2) * (NOMBRE_DE_LIGNES + 1)];
... initialisations
}
public Plateau() : this(6,10)
{
}Au passage nous avons détecté une première violation du principe DRY : la dimension du tableau Cases était codée en dur à la valeur 84, mais cette valeur doit être calculée en fonction du nombre de lignes et colonnes ci-dessus. Nous aurions pu détecter cette duplication d'information plus tôt.
Puis nous détectons une deuxième violation : la fonction de correction des décalages ne tient pas compte des dimensions du tableau final. Cette duplication était plus difficile à repérer plus tôt, car au lieu de la valeur 2 qui nous avait suffit jusque-là, il fallait la correction suivante :
correction = nombreColonnes - 10 + 2Cela nous conduit à modifier l'interface de la Fabrique de pentaminos : en effet elle doit disposer du nombre de colonnes pour fournir des pentaminos adaptés aux dimensions du plateau. Comme C# ne permet pas de valeur par défaut pour les arguments, nous sommes obligés de retoucher une douzaine d'appels à la fonction ListeDePentaminos.
Curieusement, notre test EchangeDeDimensions échoue alors. En effet il est devenu
[Test]
public void EchangeDeDimensions()
{
Algorithme algorithme = new Algorithme(new Plateau(10,6),
FabriqueDePentaminos.ListeDePentaminos(10));
Assert.That(algorithme.ChercheSolutions(), Is.EqualTo(4 * NombreSolutionsUniques));
}Dans notre correction généralisée des appels à ListeDePentaminos, nous avons hélas confondu le nombre de lignes et de colonnes dans le test. Ce qui illustre un défaut grave dans notre conception : il faut fournir deux fois le paramètre "nombre de colonnes", une fois au Plateau, et une fois à la Fabrique de pentaminos, et donc il y a fort risque d'erreur. C'est encore une violation du principe DRY. Le test illustre donc le fait que notre interface n'est pas suffisamment pratique à utiliser. Des remaniements supplémentaires sont donc nécessaires.
Nous allons nous arrêter là pour ce tutoriel ; le code obtenu permet tout de même de trouver les solutions pour une variété de plateaux (par exemple 20x3 - 8 solutions, 5x12 - 4040 solutions).
- à faible coût et faible risque, nous avons pu nous adapter à un changement de spécifications : en effet, il n'était pas prévu au départ que les dimensions du plateau changent ;
- travailler avec des tests permet de réfléchir constamment à l'interface publique de nos classes, à leur facilité d'utilisation, et à leurs éventuels défauts.
VII. Discussion▲
Remarque : dans ce tutoriel nous avons placé les classes de test au plus près des classes testées, dans le même fichier, afin de simplifier la présentation. Dans un projet professionnel, les classes de tests sont plutôt placées dans un projet à part, afin de ne pas déployer le code de tests sur les machines des clients.
VII-A. Intérêts du TDD▲
- En faisant de toutes petites étapes nous avons pu résoudre avec du code simple et propre un problème qui nous paraissait assez difficile.
- Nous avons passé très peu de temps a rechercher des bugs dans notre code ; en fait au lieu de passer du temps à examiner l'exécution de notre programme dans un debugueur, nous avons passé du temps à réfléchir à des tests. Or le temps de debug est de l'argent jeté part les fenêtres car ce temps ne profite à personne ; par contre le temps passé à écrire des tests profitera au développeur (et à ses équipiers) dans le futur car ces tests pourront être rejoués quand il faudra modifier le code. Donc le temps passé à faire du TDD est un investissement, au lieu d'être une perte.
- Chaque fois que nous avons rencontré un problème, nous avons essayé de l'isoler avec un cas de test élémentaire, afin de le reproduire et mieux le comprendre. Ceci nous a permis de faire des corrections très localisées et de portée très limitée.
- Le TDD est un support indispensable des remaniements de code, car il offre un filet de sécurité très sécurisant quand on doit modifier du code existant. Il est donc un bon complément des outils de remaniements qui sont maintenant offerts par les environnements de développement comme Visual Studio 2005, Delphi 2007 et autres.
- En nous forçant à donner des exemples d'utilisation de l'interface publique de nos classes, le TDD permet en quelque sorte de documenter cette interface, ce qui est bénéfique pour nos camarades développeurs, voire nous-mêmes quand nous revenons sur un projet quelques mois plus tard. De plus cette documentation est nécessairement parfaitement synchronisée avec le code, contrairement à des commentaires ou à une documentation papier qui ont bien souvent tendance à devenir désynchronisés avec le temps.
VII-B. Couverture de code▲
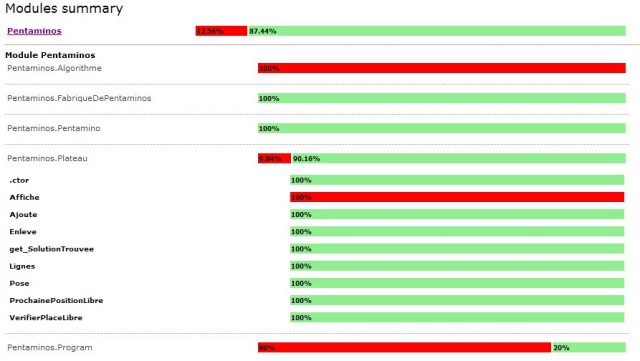
La démarche suivie a également permis d'obtenir une bonne couverture de code. Cela veut dire que durant l'exécution des tests, pratiquement tout le code écrit est exécuté, et donc vérifié. Cela ne garantit pas que notre code est correct, mais donne une mesure de la qualité de nos tests.
Pour mesurer cette couverture de code il faut utiliser un outil spécialisé comme Ncover, téléchargeable gratuitement : http://ncover.org/site/
Après installation, Ncover s'exécute comme suit:
"C:\Program Files\NCover\NCover.Console.exe" "C:\Program Files\NUnit 2.4.1\bin\nunit-console.exe" pentaminos.exeLe résultat est écrit dans un fichier nommé Coverage.xml, dont voici un extrait:
(nous avons commenté les tests fonctionnels, afin de limiter le résultat à la couverture due aux tests unitaires)
La méthode Affiche réduit la couverture de code, en effet nous n'avons aucun test qui la concerne. De même pour Main dans Program.cs. La couverture de code nous indique donc des méthodes potentiellement dangereuses car non testées.
VII-C. Complexité cyclomatique▲
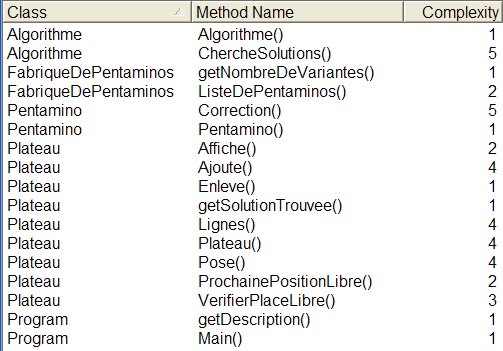
Le code produit a de plus la qualité d'avoir une faible complexité cyclomatique. Il s'agit d'une mesure du nombre de chemins d'exécution possibles dans une méthode, et cette mesure est donc proportionnelle au nombre de tests qu'il faudrait écrire pour bien couvrir une méthode donnée. Voir http://en.wikipedia.org/wiki/Cyclomatic_complexity pour une définition complète, ainsi que http://www.fromthetrench.com/cyclomatic-complexity/
De nombreux outils proposent cette mesure. Pour ce tutoriel nous avons utilisé SourceMonitor, que l'on peut obtenir gratuitement ici : http://www.campwoodsw.com/
SourceMonitor donne le résultat ci-dessous pour nos méthodes. La complexité maximum est de 5, qui est une valeur très raisonnable. En pratique, dans des projets professionnels, nous acceptons que cette complexité aille jusqu'à 8. Au-delà, les risques d'erreurs difficiles à détecter deviennent très importants, de même que le risque d'introduire des défauts supplémentaires quand on en corrige un.
VII-D. Possibilités de Nunit▲
Nous avons pu également montrer quelques possibilités de Nunit : nouvelle syntaxe pour les contraintes dans les assertions, possibilité de ranger les tests dans différentes catégories. Nous avons vu également la complémentarité des assertions traditionnelles et du TDD.
VII-E. Limites du TDD▲
- Cette démarche ne nous a pas empêché de commettre des erreurs, certaines nous ayant même privés de quelques solutions; cela montre que faire des tests unitaires ne garantit en aucune manière que l'ensemble du programme fonctionnera correctement. Il n'est donc pas possible d'éliminer le déroulement de tests fonctionnels. Si l'on ne dispose pas d'un outil spécialisé, ces tests fonctionnels peuvent être exécutés par Nunit, via par exemple les catégories de tests.
- Cette démarche ne nous a pas permis de découvrir l'algorithme de recherche de toutes les solutions; mais ceci n'est pas réellement du ressort du TDD : en effet les algorithmes astucieux se découvrent plutôt dans les salles de classes, dans les livres, sur internet ou en consultant ses collègues.
- Un certain nombre de trappes attendent le développeur qui se lance dans le TDD. Fort heureusement il existe des catalogues d'anti-patrons : par exemple nous avons traduit la liste publiée par James Carr, afin de fournir une introduction rapide à ces pièges possibles.
VIII. Conclusion▲
Nous avons essayé ici de montrer les différentes étapes d'un processus qui est extrêmement dynamique et itératif. Il s'est avéré que le traduire sous la forme statique d'un tutoriel écrit était un réel défi. Toutefois, avec ce cas concret nous espérons avoir montré que travailler en TDD permet à un développeur de gagner en sécurité et en sérénité, en ayant une grande confiance dans le code qu'il produit. Plus généralement, travailler de cette manière permet à une équipe de devenir plus performante : cela permet de mieux comprendre le code d'autrui, favorise le sentiment de propriété collective du code, augmente la confiance entre les membres de l'équipe, et contribue à réduire les tensions éventuelles.
Toutefois, en insistant surtout sur le cycle du TDD et sa discipline, nous avons ici seulement présenté la partie visible d'un iceberg. En effet en continuant à pratiquer cette discipline on constate qu'elle a une profonde influence sur le développement d'un logiciel, et qu'il faut alors approfondir diverses techniques qui facilitent le test : réduction du couplage des classes, doublures. Il faut également éviter certains écueils qui commencent maintenant a être répertoriés sous forme d'anti-patrons de tests. Enfin il reste le sujet délicat du test d'interfaces graphiques. Ces divers points pourront être abordés dans un prochain tutoriel.
Bibliographie▲
- liste d'anti-patrons de James Carr.
- Test-Driven Development: By Example de Kent Beck
Remerciements▲
- le professeur David J. Eck m'a permis de réutiliser sa structure de données modélisant les 63 variantes de pentaminos. Voir http://math.hws.edu/eck pour ses travaux sur les pentaminos (en Java).
- Laurent Gay, Emmanuel Etasse et Luc Jeanniard qui ont relu ce document et ont suggéré plusieurs améliorations.
- Les membres de Developpez.com qui ont porté ce document au gabarit officiel du site, ainsi que tous ceux qui ont répondu à mes questions dans les forums